4 posts tagged with "machine learning"

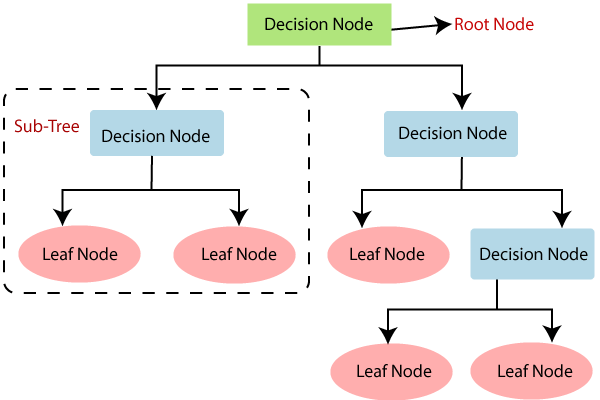
¿Que es un árbol de decisión?​

Un árbol de decisión es un modelo de predicción utilizado en el ámbito de la inteligencia artificial. Dada una base de datos se construye un árbol de decisión para poder llegar a la conclusión deseada. Es una herramienta de apoyo para la toma de decisiones.

¿Que es un método de ensamblaje?​

Los métodos de ensamblaje son métodos que combinan varios algoritmos de aprendizaje automático para obtener un mejor rendimiento predictivo que un solo algoritmo de aprendizaje automático. Los métodos de ensamblaje funcionan mejor cuando los predictores individuales están correlacionados entre sí.

Muestras con reemplazo​

En estadística, el muestreo con reemplazo es un método de muestreo en el que, para cada extracción, el elemento elegido se devuelve a la población y se mezcla con el resto de elementos. El muestreo con reemplazo es un método de muestreo no exhaustivo.

$P(x_i) = \frac{1}{N}$

En arboles de decisión se utiliza el muestreo con reemplazo para generar los árboles de decisión que se utilizaran para el ensamblaje, es decir, se generan varios árboles de decisión con muestras de la base de datos original, y se combinan para generar un modelo más robusto.

Random Forest​

Random Forest es un método de ensamblaje que combina varios árboles de decisión, cada uno de los cuales se genera con una muestra de la base de datos original, y se combinan para generar un modelo más robusto. esteme metodo usa el muestreo con reemplazo para generar los árboles de decisión.

Tenemos un datos de entrenamiento de tamaño $m$

• para b = 1 hasta B: Utilizamos el muestreo con reemplazo para generar una muestra de tamaño $m$ de la base de datos original. Entrenamos un árbol de decisión $T_b$ con la muestra generada.
• Se obtiene el modelo final combinando los $B$ árboles de decisión generados.

Cuando usamos este algorithmo, muchas veces tenemos la misma división en el nodo raíz, por lo que podemos modificar un poco el algorithmo para que esto no suceda, y así obtener un mejor modelo.

Elección de características aleatorias​

En cada nodo, se elige un subconjunto aleatorio de $k$ características de todo el conjunto de características. si $n$ es el número total de características, se recomienda $k = \sqrt{n}$ para la regresión y $k = \frac{n}{3}$ para la clasificación, debe de tener en cuenta que esto es recomendado para un gran número de características

XGBoost ( ExTreme Gradient Boosting)​

XGBoost es un método de ensamblaje que combina varios árboles de decisión, cada uno de los cuales se genera con una muestra de la base de datos original, y se combinan para generar un modelo más robusto. este metodo usa el muestreo con reemplazo para generar los árboles de decisión.

Pero a diferencia de Random Forest, XGBoost utiliza un algorithmo de optimización para generar los árboles de decisión, En vez de utilizar el muestreo con reemplazo para generar los árboles de decisión con una probabilidad uniforme $1/m$, XGBoost utiliza un algorithmo de optimización para generar los árboles de decisión con una probabilidad $p_i$ que depende de la pérdida de la iteración anterior.

$p_i = \frac{e^{\frac{-\Delta L_i}{\lambda}}}{\sum_{i=1}^{m} e^{\frac{-\Delta L_i}{\lambda}}}$

Donde:

• $\Delta L_i$ es la pérdida de la iteración $i$
• $\lambda$ es un parámetro de regularización

La idea de esto es que el algorithmo de optimización se enfoque en las muestras que tienen una pérdida mayor, y así generar un mejor modelo.

Ventajas de XGBoost​

• Implementaciónes open source en varios lenguajes de programación
• Rapidez en el entrenamiento
• Buena elección de divisiónes criticas por defecto y criterio para cuando parar de dividir
• Regularización para evitar el sobreajuste

Implementación en Python​

Para la implementación en Python, se utilizara la librería XGBoost, la cual se puede instalar con el comando:

from xgboost import XGBClassifier
model = XGBClassifier() # XGBRegressor para regresión
model.fit(X_train, y_train)
y_pred = model.predict(X_test)

Cuando usar Arboles de decisión y métodos de ensamblaje​

• Trabajan bien con datos tabulares (estructurados)
• No se recomienda para datos no estructurados (imágenes, texto, audio, etc)
• Es muy rápido en entrenamiento y predicción
• Pequeños arboles de decisión son fáciles de interpretar (visualizar)

Cuando usar neural networks​

• Trabaja bien con todo tipo de datos tabulares "estructurados" y "no estructurados"
• Puede ser lento en entrenamiento y predicción
• Trabaja con transfer learning
• Cuando trabajamos con multiples modelos juntos, puede ser mas sencillo encadenarlos con una red neuronal

La detección de anomalías es el proceso de identificar patrones inusuales en los datos. Es un problema de aprendizaje no supervisado, lo que significa que no necesitamos tener etiquetas para entrenar nuestro modelo. En cambio, nuestro modelo aprenderá a identificar patrones inusuales en los datos por sí mismo.

La detección de anomalías se puede aplicar a una amplia gama de dominios, como la detección de fraudes con tarjetas de crédito, la detección de fallas en equipos de fabricación o la detección de anomalías médicas.

Estimación de densidad​

La detección de anomalías se puede realizar utilizando un modelo de estimación de densidad. La idea es que los datos normales se distribuirán de manera diferente a los datos anormales. Por lo tanto, podemos estimar la densidad de los datos normales y luego identificar los puntos de datos que tienen una densidad significativamente menor como anomalías.

Dado el conjunto de datos de entrenamiento $\{x^{(1)}, x^{(2)}, \ldots, x^{(m)} \}$, donde cada ejemplo tiene $n$ características, podemos estimar la densidad de los datos como:

$p(x) = p(x_1; \mu_1, \sigma_1^2) \times p(x_2; \mu_2, \sigma_2^2) \times \ldots \times p(x_n; \mu_n, \sigma_n^2)$ $= \prod_{j=1}^n p(x_j; \mu_j, \sigma_j^2)$

Algoritmo de detección de anomalías​

1. Elija las características $x_i$ que crea que pueden indicar anomalías.

2. Ajuste los parámetros $\mu_1, \ldots, \mu_n, \sigma_1^2, \ldots, \sigma_n^2$ en el conjunto de entrenamiento $\{x^{(1)}, x^{(2)}, \ldots, x^{(m)} \}$. $\vec{\mu} = \frac{1}{m} \sum_{i=1}^m \vec{x^{(i)}}$ $\vec{\sigma^2} = \frac{1}{m} \sum_{i=1}^m (\vec{x^{(i)}} - \vec{\mu})^2$

3. Dado un nuevo ejemplo $x$, compute $p(x)$:

$p(x) = \prod_{j=1}^n p(x_j; \mu_j, \sigma_j^2) = \prod_{j=1}^n \frac{1}{\sqrt{2\pi}\sigma_j} \exp \left( - \frac{(x_j - \mu_j)^2}{2\sigma_j^2} \right)$

1. Si $p(x) < \epsilon$, marque un ejemplo de anomalía.

Escoger que caracteristicas usar​

En Deteción de Anomalías, se debe escoger que caracteristicas usar, ya que si se usan todas las caracteristicas, el algoritmo no funcionará correctamentem.

Caracteristicas no gaussianas​

Cuando encontramos caracteristicas que no son gaussianas, se debe aplicar una transformación a los datos para que se vuelvan gaussianos.

por ejemplo:

• $x_1 = \log(x_1)$
• $x_2 = \log(x_2 + c)$
• $x_3 = \sqrt{x_3}$
• $x_4 = x_4^{1/3}$

En python

from scipy.stats import skewnorm
import matplotlib.pyplot as plt

numValues = 1000
maxValue = 100
skewness = 20

randomValues = skewnorm.rvs(a=skewness, loc=maxValue, size=numValues)

randomValues = randomValues - min(randomValues) # cambia el conjunto de datos para que comience en 0
randomValues = randomValues / max(randomValues) # cambia el conjunto de datos para que termine en 1
randomValues = randomValues * maxValue # cambia el conjunto de datos para que termine en maxValue

x = randomValues

fig, ax = plt.subplots(1, 3, figsize=(15, 5))

ax[0].hist(x, bins=50)
ax[0].set_title('X')

# x**2
ax[1].hist(x**2, bins=50)
ax[1].set_title('X^2')

# x**0.4
ax[2].hist(x**0.4, bins=50)
ax[2].set_title('X^0.4')

plt.show()

Error en el analisis para detección de anomalías​

El problema más común en la detección de anomalías es que el conjunto de datos de entrenamiento contiene muy pocos ejemplos de anomalías. Por lo tanto, el algoritmo de detección de anomalías no puede aprender lo suficiente sobre los ejemplos de anomalías para identificarlos correctamente en el conjunto de prueba.

¿Que es clustering?​

Clustering es un método de aprendizaje no supervisado, que consiste en agrupar un conjunto de objetos de tal manera que los objetos del mismo grupo (o cluster) sean más similares (en algún sentido o en algún aspecto) entre sí que los de otros grupos.

k-means​

k-means es un algoritmo de clustering que consiste en agrupar un conjunto de objetos de tal manera que los objetos del mismo grupo (o cluster) sean más similares (en algún sentido o en algún aspecto) entre sí que los de otros grupos.

Algoritmo de k-means​

1. Inicializar los centroides de los clusters aleatoriamente (k puntos): $\mu_1, \mu_2, ..., \mu_k$

k-means optimización objetivo​

• $c^{(i)}$ = índice del cluster (1, 2, ..., k) al que se asigna el ejemplo $x^{(i)}$
• $u_k$ = vector de parámetros del centroide del cluster $k$
• $\mu_{c^{(i)}}$ = vector de parámetros del centroide del cluster al que se asigna el ejemplo $x^{(i)}$

Función de costo

$J(c^{(1)}, ..., c^{(m)}, \mu_1, ..., \mu_k) = \frac{1}{m} \sum_{i=1}^{m} ||x^{(i)} - \mu_{c^{(i)}}||^2$

Objetivo: Encontrar $c^{(1)}, ..., c^{(m)}, \mu_1, ..., \mu_k$ que minimicen $J$.

$min_{c^{(1)}, ..., c^{(m)}, \mu_1, ..., \mu_k} J(c^{(1)}, ..., c^{(m)}, \mu_1, ..., \mu_k)$

Inicializando k-means​

• Seleccionar aleatoriamente $k$ ejemplos de entrenamiento $x^{(1)}, ..., x^{(k)}$ que servirán como los centroides iniciales: $\mu_1, ..., \mu_k$.

Elección del número de clusters​

¿Cual es el número de clusters óptimo?

Para elegir el número de clusters óptimo se puede utilizar los siguientes 2 métodos:

• Método del codo: el metodo del codo consiste en graficar el valor de la función de costo $J$ en función del número de clusters $k$. El número de clusters óptimo será el valor de $k$ en el que la función de costo $J$ se "quiebre" o tenga un cambio de pendiente más pronunciado.

No es una buena métrica para elegir el número de clusters óptimo, ya que no siempre se puede identificar un cambio de pendiente claro en la gráfica, no hay un codo claro.

la elección del número de clusters es subjetiva, depende de la aplicación y del contexto.

Modelo de arbol de desición​

Un árbol de decisión es un modelo de predicción utilizado en el ámbito de la inteligencia artificial, que utiliza un árbol de estructura similar a los diagramas de flujo en donde cada nodo representa una característica (o atributo), cada rama representa una regla de decisión y cada hoja representa el resultado de una decisión. Los árboles de decisión son utilizados comúnmente en minería de datos con el fin de resolver problemas de clasificación.

Ejemplo de un arbol de desición y su estructura:

Entropía​

¿Qué es la entropía?​

La entropía es una medida de incertidumbre. En el contexto de la toma de decisiones, la entropía mide la impureza de un conjunto de ejemplos S. Si S solo contiene ejemplos de una clase, entonces la entropía es 0. Si S contiene una cantidad uniforme de ejemplos de cada clase, entonces la entropía es 1. La entropía de un conjunto S se denota por H (S).

¿Cómo se calcula la entropía?​

La entropía de un conjunto S se calcula como:

$H(S) = -\sum_{i=1}^{c} p_i log_2 p_i$

Donde:

• $c$ es el número de clases
• $p_i$ es la proporción de ejemplos de clase $i$ en $S$
• $log_2$ es el logaritmo en base 2

Ejemplo de cálculo de entropía​

Supongamos que tenemos un conjunto de ejemplos $S$ con 14 ejemplos de clase 1 y 6 ejemplos de clase 2. La entropía de $S$ es:

$P_1 = 14/20$ y $P_2 = 6/20$

Entonces, la entropía de $S$ sería: $H(S) = - \left(\frac{14}{20} \log_2 \frac{14}{20} + \frac{6}{20} \log_2 \frac{6}{20}\right) \approx 0.88$.

Ganancia de información​

La ganancia de información(IG) se utiliza para decidir qué atributo se utilizará para dividir el conjunto de datos en subconjuntos homogéneos. La ganancia de información se define como la diferencia entre la entropía antes de la división y la entropía después de la división por un atributo. La ganancia de información se denota por IG (S, A) y se calcula como:

$IG(S, A) = H(S) - \sum_{v \in Values(A)} \frac{|S_v|}{|S|} H(S_v)$

Donde:

• $S$ es el conjunto de ejemplos
• $A$ es el atributo utilizado para dividir $S$ en subconjuntos
• $Values(A)$ es el conjunto de valores que puede tomar el atributo $A$
• $S_v$ es el subconjunto de $S$ en el que el atributo $A$ tiene el valor $v$

Indice Gini​

El índice de Gini es una medida de impureza utilizada en los árboles de decisión para decidir qué atributo dividir un nodo en dos o más subnodos. El índice de Gini se define como:

$Gini(S) = 1 - \sum_{i=1}^{c} p_i^2$

Donde:

• $c$ es el número de clases
• $p_i$ es la proporción de ejemplos de clase $i$ en $S$

Pros y contras de los árboles de decisión​

Pros​

• Fácil de entender e interpretar. Los árboles se pueden visualizar.
• Puede ser muy util para solucionar problemas relacionados con decisiones.
• Hay menos requisitos de limpieza de datos

Contras​

• Los árboles de decisión pueden ser poco precisos. Pueden ser muy sensibles a pequeños cambios en los datos.