Cheat Sheets de Pandas reshaping

August 16, 2023 · One min read

pivot

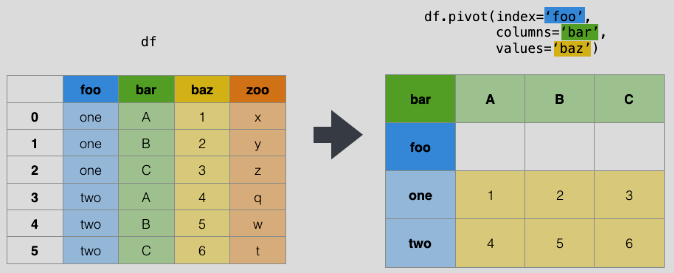
Alt text

df.pivot(index='foo', columns='bar', values='baz')

df.pivot_table(index='foo', columns='bar', values='baz', aggfunc='sum')

melt

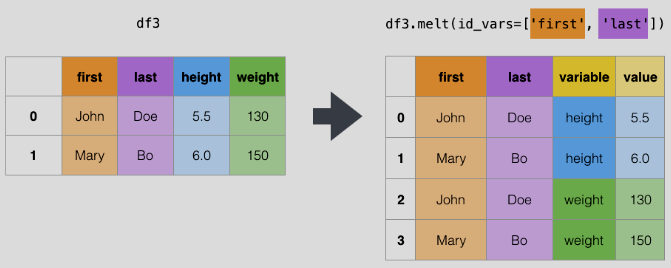
Alt text

df3.melt(id_vars=['first', 'last'], var_name='variable', 
        value_name='value')
df3.melt(id_vars=['first', 'last'], var_name='variable', 
        value_name='value', value_vars=['height', 'weight'])

Wide to long

Alt text

pd.wide_to_long(df, stubnames=['age', 'weight'], i=['name'], 
                j='year')
# format age_2019
pd.wide_to_long(df, stubnames=['age', 'weight'], i=['name'], 
                j='year', sep='_', suffix='\w+')

Cheat Sheets

August 16, 2023 · One min read

Probando el componente CheatSheet con diferentes lenguajes de programación y latex.

Titulo

Contenido de la cheat sheet

import CheatSheet from '@site/src/components/CheatSheet';
<CheatSheet header='Titulo'>
    Contenido de la cheat sheet
</CheatSheet>

Contenido de latext

Formula en latex $\int_{a}^{b} x^2 dx$

$$\int_{a}^{b} x^2 dx$$

Multiples lenguajes

Contenido de la cheat sheet

def foo():
    print('Hello world!')

foo <- function() {
    print('Hello world!')
}

Fomulas y codigo

Formula en latex $\int_{a}^{b} x^2 dx$

def foo():
    print('Hello world!')

Imagenes

Alt text

Sin titulo

<CheatSheet>
    Sin titulo
</CheatSheet>

Header

Texto en latex

\int_{a}^{b} x^2 dx

$\int_{a}^{b} x^2 dx$

Header

Código python

def foo():
    print('Hello world!')

Linear models in scikit-learn

August 16, 2023 · 3 min read

Darvin Cotrina

Creador de entredata.org

Linear Model

The following linear models are available in scikit-learn for regression and classification tasks, if $y$ is the target variable, $x$ is the feature vector, and $w$ is the weight vector
$y = w_0 + w_1x_1 + w_2x_2 + ... + w_px_p$

$w_0$ is the intercept_
$w_1, w_2, ..., w_p$ are the coef_

Linear Regression

Fits a linear model with coefficients $w = (w1, …, wp)$ to minimize the residual sum of squares between the observed targets in the dataset, and the targets predicted by the linear approximation.
$\min_{w} || X w - y||_2^2$

from sklearn.linear_model import LinearRegression
lr = LinearRegression()

Ridge Regression

Applies L2 regularization to reduce the complexity of the model and prevent overfitting.
$\min_{w} || X w - y||_2^2 + \alpha ||w||_2^2$
Hyperparameter $\alpha$

if $\alpha = 0$ , then the model is the same as Linear Regression

from sklearn.linear_model import Ridge
ridge = Ridge(alpha=1.0)

from sklearn.linear_model import RidgeCV 

Lasso Regression

Applies L1 regularization to reduce the complexity of the model and prevent overfitting.
$\min_{w} || X w - y||_2^2 + \alpha ||w||_1$
Hyperparameter $\alpha$

if $\alpha = 0$ , then the model is the same as Linear Regression

from sklearn.linear_model import Lasso
lasso = Lasso(alpha=1.0)

Elastic Net Regression

Applies both L1 and L2 regularization to reduce the complexity of the model and prevent overfitting.
$\min_{w} || X w - y||_2^2 + \alpha \rho ||w||_1 + \frac{\alpha(1-\rho)}{2} ||w||_2^2$
Hyperparameter $\alpha$ and $l1\_ratio$

if $\alpha = 0$ , and $l1\_ratio = 0$ , then the model is the same as Linear Regression

from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=1.0, l1_ratio=0.5)

Polynomial Regression

Generates polynomial features and fits a linear model to the transformed data.
$y = w_0 + w_1x_1 + w_2x_2 + w_3x_1^2 + w_4x_1x_2 + w_5x_2^2 + ...$
Hyperparameter degree

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline

poly = PolynomialFeatures(degree=2)
poly_reg = make_pipeline(poly, LinearRegression())

Logistic Regression

Use when you want to predict a binary outcome (0 or 1, yes or no, true or false) given a set of independent variables.
$y = \frac{1}{1 + e^{-(w_0 + w_1x_1 + w_2x_2 + ... + w_px_p)}}$

from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()

Stocastic Gradient Descent

Use when you want to train large datasets.
$w_{t+1} = w_t - \eta \nabla Q_i(w_t)$
Hyperparameter eta0 is the learning rate

from sklearn.linear_model import SGDClassifier, SGDRegressor
sgd_clf = SGDClassifier()
sgd_reg = SGDRegressor()

Bayesian Ridge Regression

Bayesian Ridge Regression is similar to Ridge Regression, but it introduces a prior on the weights $w$ .
Original Algorithm is detailed in the book Bayesian learning for neural networks
Hyperparameter alpha_1, alpha_2, lambda_1, lambda_2

from sklearn.linear_model import BayesianRidge
bayesian_ridge = BayesianRidge()

Passive Aggressive

Passive Aggressive algorithms are a family of algorithms for large-scale learning

from sklearn.linear_model import PassiveAggressiveClassifier, PassiveAggressiveRegressor
passive_aggressive_clf = PassiveAggressiveClassifier()
passive_aggressive_reg = PassiveAggressiveRegressor()

RANSAC Regression

RANSAC (RANdom SAmple Consensus) is an iterative algorithm for the robust estimation of parameters from a subset of inliers from the complete data set.

from sklearn.linear_model import RANSACRegressor
ransac_reg = RANSACRegressor()

Muestreo con python

July 9, 2023 · 2 min read

Darvin Cotrina

Creador de entredata.org

import numpy as np
import pandas as pd
from scipy import stats

Muestreo aleatorio

np.random.random(10)
np.random.randint(0, 100, 10)
colors = ['red', 'blue', 'green']
np.random.choice(colors, 10)

Con reemplazo

np.random.choice(colors, 10, replace=True)

Distribucion normal

parametros: $\mu$ media, $\sigma$ desviacion estandar y $n$ tamaño de la muestra

np.random.normal(0, 1, 10)

stats.norm.rvs(0, 1, 10)

Distribucion uniforme

parametros: $a$ minimo, $b$ maximo y $n$ tamaño de la muestra

np.random.uniform(0, 1, 10)

stats.uniform.rvs(0, 1, 10)

Distribucion binomial

parametros: $n$ numero de ensayos, $p$ probabilidad de exito y $n$ tamaño de la muestra

np.random.binomial(10, 0.5, 10)

stats.binom.rvs(10, 0.5, 10)

Distribucion poisson

parametros: $\lambda$ tasa de ocurrencia y $n$ tamaño de la muestra

np.random.poisson(10, 10)

stats.poisson.rvs(10, 10)

Distribucion exponencial

parametros: $\lambda$ tasa de ocurrencia y $n$ tamaño de la muestra

np.random.exponential(10, 10)

stats.expon.rvs(10, 10)

Muestreo estratificado

df = pd.DataFrame({
    'sexo': np.random.choice(['M', 'F'], 100),
    'edad': np.random.randint(18, 65, 100),
    'estado_civil': np.random.choice(['S', 'C', 'D', 'V'], 100),
    'ingreso': np.random.randint(1000, 10000, 100)
})

df.groupby('sexo').apply(lambda x: x.sample(10))

Muestreo sistematico

df = pd.DataFrame({
    'sexo': np.random.choice(['M', 'F'], 100),
    'edad': np.random.randint(18, 65, 100),
    'estado_civil': np.random.choice(['S', 'C', 'D', 'V'], 100),
    'ingreso': np.random.randint(1000, 10000, 100)
})

df.iloc[::10] # selecciona cada 10 filas

Importar datos de diferentes fuentes con Python

July 7, 2023 · 2 min read

Darvin Cotrina

Creador de entredata.org

Flat files

CSV

import pandas as pd
# puede ser un file o una url
pd.read_csv('file.csv') 
pd.read_csv('file.txt', sep='\t')

Excel

import pandas as pd
# puede ser un file o una url
# en caso de que sheetname, no este asignado, se lee la primera hoja
xls = pd.ExcelFile('file.xlsx', sheetname=None) # Leer todas las hojas
xls.keys() # Nombre de las hojas
xls['sheet'] # Leer hoja

SAS

from sas7bdat import SAS7BDAT
with SAS7BDAT('file.sas7bdat') as file:
    df_sas = file.to_data_frame()

Stata

import pandas as pd
# puede ser un file o una url
df = pd.read_stata('file.dta')

HDF5

Los archivos HDF5 son una buena opción para guardar grandes cantidades de datos. Se pueden leer con la librería h5py

import h5py
data = h5py.File('file.hdf5', 'r')
data.keys() # Nombre de los grupos

group = data['group'] # Leer grupo
group.keys() # Nombre de los datasets

dataset = group['dataset'] # Leer dataset
dataset.shape # Dimensiones
dataset.value # Valores

Matlab

import scipy.io
mat = scipy.io.loadmat('file.mat')

Pickled files

Los archivos pickled son archivos binarios de Python. Se pueden leer con la librería pickle

import pickle
with open('file.pkl', 'rb') as file:
    data = pickle.load(file)

SQL

from sqlalchemy import create_engine
engine = create_engine('sqlite:///file.sqlite')
table_names = engine.table_names() # Nombre de las tablas

with engine.connect() as con:
    rs = con.execute('SELECT * FROM table')
    df = pd.DataFrame(rs.fetchall())
    df.columns = rs.keys()

Con Pandas

import pandas as pd
from sqlalchemy import create_engine
engine = create_engine('sqlite:///file.sqlite')

df = pd.read_sql_query('SELECT * FROM table', engine)

Preprocesamiento de datos para machine learning

July 5, 2023 · 3 min read

Darvin Cotrina

Creador de entredata.org

Missing data

Es importante tener en cuenta que los modelos de machine learning no pueden trabajar con valores nulos, por lo que es necesario reemplazarlos por algún valor.

Eliminar

Si hay muchos valores nulos, se puede eliminar la columna o fila, tener en cuenta que se puede perder información importante.

df.dropna()

Imputar

from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy='mean')
imputer.fit_transform(X)

crear columna indicadora

from sklearn.impute import MissingIndicator
indicator = MissingIndicator()
indicator.fit_transform(X)

Encoder data

Dummy

Variable	Dummy
color	color_rojo	color_verde	color_azul
rojo	1	0	0
verde	0	1	0
azul	0	0	1

from sklearn.preprocessing import OneHotEncoder
encoder = OneHotEncoder()
encoder.fit_transform(X)

import pandas as pd
pd.get_dummies(X)

Label

Variable	Label
rojo	0
verde	1
azul	2

```python from sklearn.preprocessing import LabelEncoder encoder = LabelEncoder() encoder.fit_transform(X) ```

import pandas as pd
df = pd.DataFrame({'color': ['rojo', 'verde', 'azul']})
df['color'].astype('category').cat.codes

Scaling and Centering Data

StandardScaler

$\frac{x - \mu}{\sigma}$

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit_transform(X)

MinMaxScaler

$\frac{x - min}{max - min}$

from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit_transform(X)

RobustScaler

$\frac{x - Q_1}{Q_3 - Q_1}$

from sklearn.preprocessing import RobustScaler
scaler = RobustScaler()
scaler.fit_transform(X)

Normalizer

L1: $\frac{x}{\sum_{i=1}^n |x_i|}$
L2: $\frac{x}{\sqrt{\sum_{i=1}^n x_i^2}}$
max: $\frac{x}{max(x)}$

from sklearn.preprocessing import Normalizer
# L1, L2, max
scaler = Normalizer(norm='l2')
scaler.fit_transform(X)

Feature engineering

PolynomialFeatures

$x_1, x_2 \rightarrow x_1^2, x_1x_2, x_2^2$

from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2)
poly.fit_transform(X)

Binning

Este proceso se utiliza para discretizar variables continuas, es decir, convertir variables continuas en variables categóricas, agrupando los valores en intervalos.

$x \rightarrow \{0, 1, 2,..., n\}$

from sklearn.preprocessing import KBinsDiscretizer
discretizer = KBinsDiscretizer(n_bins=3, encode='ordinal', strategy='uniform')
discretizer.fit_transform(X)

Feature selection

VarianceThreshold

from sklearn.feature_selection import VarianceThreshold
selector = VarianceThreshold(threshold=0.1)
selector.fit_transform(X)

SelectKBest

from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
selector = SelectKBest(chi2, k=2)
selector.fit_transform(X, y)

SelectFromModel

from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression
selector = SelectFromModel(estimator=LogisticRegression())
selector.fit_transform(X, y)

RFE

from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression
selector = RFE(estimator=LogisticRegression(), n_features_to_select=2)
selector.fit_transform(X, y)

Metricas para evaluar un modelo en machine learning

July 3, 2023 · 3 min read

Darvin Cotrina

Creador de entredata.org

Classification Metrics

Confusion Matrix

	Predicted
Actual class	Positive	Negative
Positive	True Positive (TP)	False Negative (FN)
Negative	False Positive (FP)	True Negative (TN)

from sklearn.metrics import confusion_matrix
confusion_matrix(y_true, y_pred)

Accuaracy

Usar Accuaracy cuando quieres medir la performance de un modelo de clasificacion. Es la proporcion de predicciones correctas sobre el total de predicciones realizadas.

Accuracy = $\frac{TP + TN}{TP + TN + FP + FN}$

from sklearn.metrics import accuracy_score
accuracy_score(y_true, y_pred)

Precision

Usar Precision cuanto quieres minimizar los falsos positivos (Errores de tipo I). Es la proporcion de predicciones correctas sobre el total de predicciones realizadas.

Precision = $\frac{TP}{TP + FP}$

from sklearn.metrics import precision_score
precision_score(y_true, y_pred)

Recall

Usar Recall cuando quieres minimizar los falsos negativos (Errores de tipo II). Es la proporcion de predicciones correctas sobre el total de predicciones realizadas.

Recall = $\frac{TP}{TP + FN}$

from sklearn.metrics import recall_score
recall_score(y_true, y_pred)

F1 Score

Usar F1 Score cuando quieres minimizar los falsos negativos y falsos positivos. Es la media armonica entre Precision y Recall.

F1 Score = $\frac{2 * Precision * Recall}{Precision + Recall}$

from sklearn.metrics import f1_score
f1_score(y_true, y_pred)

ROC Curve

Usar ROC Curve cuando quieres evaluar el rendimiento de un modelo de clasificacion binaria. Es una grafica de la tasa de verdaderos positivos (TPR) frente a la tasa de falsos positivos (FPR) para diferentes umbrales de probabilidad de clasificacion.

TPR = $\frac{TP}{TP + FN}$
FPR = $\frac{FP}{FP + TN}$

from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib.pyplot as plt

fpr, tpr, thresholds = roc_curve(y_true, y_pred)
auc = roc_auc_score(y_true, y_pred)

plt.plot(fpr, tpr, label='ROC curve (area = %0.2f)' % auc)
plt.plot([0, 1], [0, 1], 'k--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.show()

Classification Report

Usar Classification Report cuando quieres evaluar el rendimiento de un modelo de clasificacion. Es un resumen de las metricas de clasificacion para cada clase del problema.

from sklearn.metrics import classification_report
print(classification_report(y_true, y_pred))

Regression Metrics

Mean Absolute Error (MAE)

Usar MAE cuando quieres medir el error medio de un modelo de regresion. Es la media de la diferencia absoluta entre las predicciones y los valores reales.

MAE = $\frac{1}{n} \sum_{i=1}^{n} |y_{i} - \hat{y}_{i}|$

from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_true, y_pred)

Mean Squared Error (MSE)

Usar MSE cuando quieres penalizar los errores mas grandes. Es la mejor metrica cuando le preocupa las grandes desviaciones en los errores.

MSE = $\frac{1}{n} \sum_{i=1}^{n} (y_{i} - \hat{y}_{i})^{2}$

from sklearn.metrics import mean_squared_error
mean_squared_error(y_true, y_pred)

Root Mean Squared Error (RMSE)

Usar RMSE cuando quieres penalizar los errores mas grandes. Es la mejor metrica cuando desea una medida que sea menos sensible a los valores atipicos.

RMSE = $\sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_{i} - \hat{y}_{i})^{2}}$

from sklearn.metrics import mean_squared_error
mean_squared_error(y_true, y_pred, squared=False)
# or
import numpy as np
np.sqrt(mean_squared_error(y_true, y_pred))

R-Squared (R2)

Usar R2 cuando quieres medir la varianza de los errores. Es la proporcion de la varianza de los errores y la varianza de los valores reales

R2 = $1 - \frac{\sum_{i=1}^{n} (y_{i} - \hat{y}_{i})^{2}}{\sum_{i=1}^{n} (y_{i} - \bar{y}_{i})^{2}}$

from sklearn.metrics import r2_score
r2_score(y_true, y_pred)

pivot

melt

Wide to long

Titulo

Contenido de latext

Multiples lenguajes

Fomulas y codigo

Imagenes

Header

Header

Linear Model

Linear Regression

Ridge Regression

Lasso Regression

Elastic Net Regression

Polynomial Regression

Logistic Regression

Stocastic Gradient Descent

Bayesian Ridge Regression

Passive Aggressive

RANSAC Regression

Muestreo aleatorio

Con reemplazo​

Distribucion normal

Distribucion uniforme

Distribucion binomial

Distribucion poisson

Distribucion exponencial

Muestreo estratificado

Muestreo sistematico

Flat files

CSV​

Excel

SAS

Stata

HDF5

Matlab

Pickled files

SQL

Con Pandas​

Missing data

Eliminar​

Imputar​

crear columna indicadora

Encoder data

Dummy​

Label​

Scaling and Centering Data

StandardScaler​

MinMaxScaler​

RobustScaler​

Normalizer​

Feature engineering

PolynomialFeatures​

Binning​

Feature selection

VarianceThreshold​

SelectKBest​

SelectFromModel​

RFE​

Classification Metrics​

Confusion Matrix

Accuaracy

Precision

Recall

F1 Score

ROC Curve

Classification Report

Regression Metrics​

Mean Absolute Error (MAE)

Mean Squared Error (MSE)

Root Mean Squared Error (RMSE)

R-Squared (R2)

Con reemplazo

CSV

Con Pandas

Eliminar

Imputar

Dummy

Label

StandardScaler

MinMaxScaler

RobustScaler

Normalizer

PolynomialFeatures

Binning

VarianceThreshold

SelectKBest

SelectFromModel

RFE

Classification Metrics

Regression Metrics