Detección de anomalías

La detección de anomalías es el proceso de identificar patrones inusuales en los datos. Es un problema de aprendizaje no supervisado, lo que significa que no necesitamos tener etiquetas para entrenar nuestro modelo. En cambio, nuestro modelo aprenderá a identificar patrones inusuales en los datos por sí mismo.

La detección de anomalías se puede aplicar a una amplia gama de dominios, como la detección de fraudes con tarjetas de crédito, la detección de fallas en equipos de fabricación o la detección de anomalías médicas.

Estimación de densidad

La detección de anomalías se puede realizar utilizando un modelo de estimación de densidad. La idea es que los datos normales se distribuirán de manera diferente a los datos anormales. Por lo tanto, podemos estimar la densidad de los datos normales y luego identificar los puntos de datos que tienen una densidad significativamente menor como anomalías.

Dado el conjunto de datos de entrenamiento $\{x^{(1)}, x^{(2)}, \ldots, x^{(m)} \}$, donde cada ejemplo tiene $n$ características, podemos estimar la densidad de los datos como:

$p(x) = p(x_1; \mu_1, \sigma_1^2) \times p(x_2; \mu_2, \sigma_2^2) \times \ldots \times p(x_n; \mu_n, \sigma_n^2)$ $= \prod_{j=1}^n p(x_j; \mu_j, \sigma_j^2)$

Algoritmo de detección de anomalías

1. Elija las características $x_i$ que crea que pueden indicar anomalías.

2. Ajuste los parámetros $\mu_1, \ldots, \mu_n, \sigma_1^2, \ldots, \sigma_n^2$ en el conjunto de entrenamiento $\{x^{(1)}, x^{(2)}, \ldots, x^{(m)} \}$. $\vec{\mu} = \frac{1}{m} \sum_{i=1}^m \vec{x^{(i)}}$ $\vec{\sigma^2} = \frac{1}{m} \sum_{i=1}^m (\vec{x^{(i)}} - \vec{\mu})^2$

3. Dado un nuevo ejemplo $x$, compute $p(x)$:

$p(x) = \prod_{j=1}^n p(x_j; \mu_j, \sigma_j^2) = \prod_{j=1}^n \frac{1}{\sqrt{2\pi}\sigma_j} \exp \left( - \frac{(x_j - \mu_j)^2}{2\sigma_j^2} \right)$

1. Si $p(x) < \epsilon$, marque un ejemplo de anomalía.

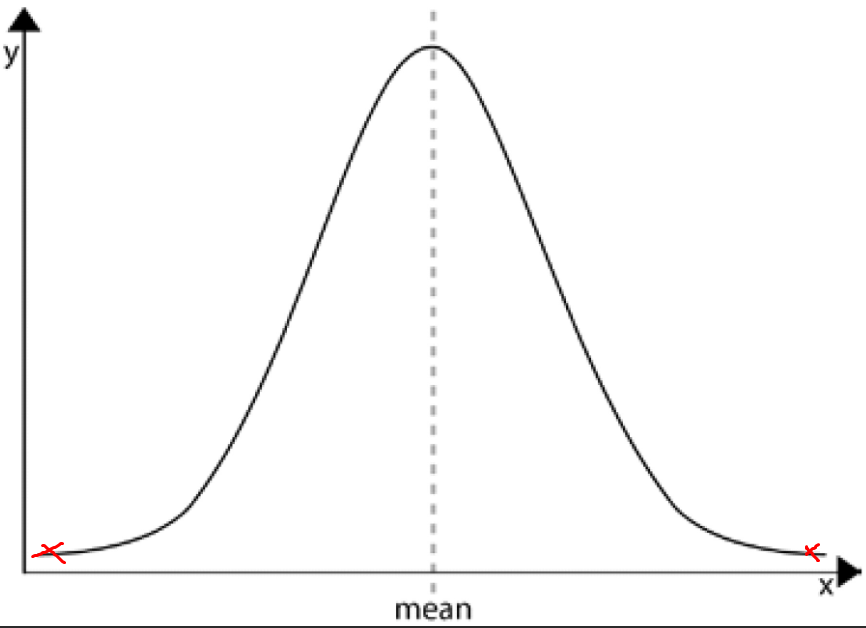
Escoger que caracteristicas usar

En Deteción de Anomalías, se debe escoger que caracteristicas usar, ya que si se usan todas las caracteristicas, el algoritmo no funcionará correctamentem.

Caracteristicas no gaussianas

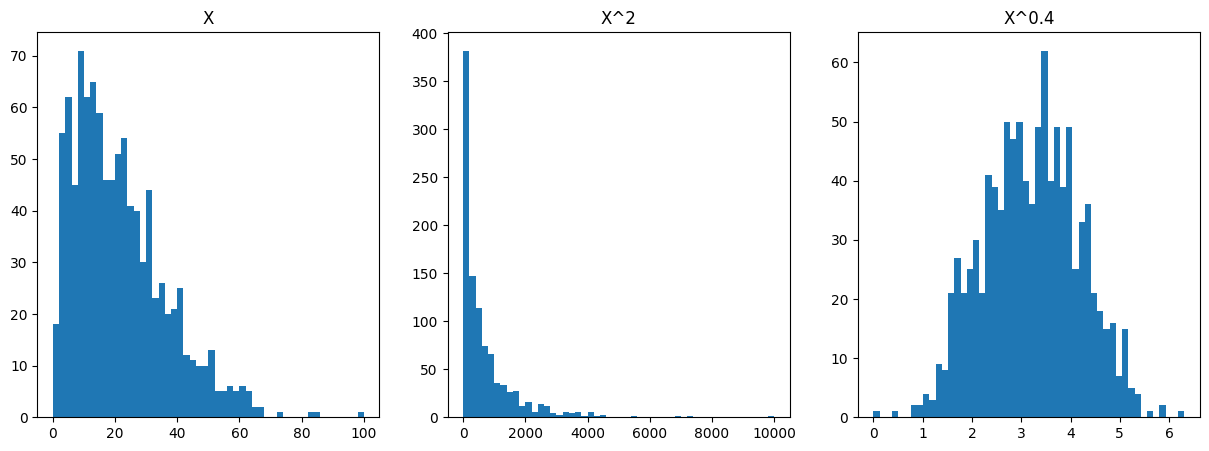
Cuando encontramos caracteristicas que no son gaussianas, se debe aplicar una transformación a los datos para que se vuelvan gaussianos.

por ejemplo:

• $x_1 = \log(x_1)$
• $x_2 = \log(x_2 + c)$
• $x_3 = \sqrt{x_3}$
• $x_4 = x_4^{1/3}$

En python

from scipy.stats import skewnorm
import matplotlib.pyplot as plt

numValues = 1000
maxValue = 100
skewness = 20

randomValues = skewnorm.rvs(a=skewness, loc=maxValue, size=numValues)

randomValues = randomValues - min(randomValues) # cambia el conjunto de datos para que comience en 0
randomValues = randomValues / max(randomValues) # cambia el conjunto de datos para que termine en 1
randomValues = randomValues * maxValue # cambia el conjunto de datos para que termine en maxValue

x = randomValues

fig, ax = plt.subplots(1, 3, figsize=(15, 5))

ax[0].hist(x, bins=50)
ax[0].set_title('X')

# x**2
ax[1].hist(x**2, bins=50)
ax[1].set_title('X^2')

# x**0.4
ax[2].hist(x**0.4, bins=50)
ax[2].set_title('X^0.4')

plt.show()

Error en el analisis para detección de anomalías

El problema más común en la detección de anomalías es que el conjunto de datos de entrenamiento contiene muy pocos ejemplos de anomalías. Por lo tanto, el algoritmo de detección de anomalías no puede aprender lo suficiente sobre los ejemplos de anomalías para identificarlos correctamente en el conjunto de prueba.