¿Que es una Siamese Network?
Es un tipo especial de arquitecura de red neuronal que permite comparar dos imagenes y determinar si son similares o no, la caracteristica principal de este tipo de red es que comparten los mismos pesos y arquitectura, es decir, son dos redes neuronales que comparten los mismos pesos y arquitectura, esto permite que la red pueda aprender a comparar dos imagenes y determinar si son similares o no.
Importar modulos
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import random
Preparar los datos
(X_train, y_train), (X_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
# cast to float32
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
print('fashion_mnist train shape:', X_train.shape)
print('fashion_mnist test shape:', X_test.shape)
# normalize data
X_train /= 255.
X_test /= 255.
fashion_mnist train shape: (60000, 28, 28)
fashion_mnist test shape: (10000, 28, 28)
Crear nuestros pares de datos positivos y negativos
- Pares positivos: Dos imágenes que contienen las mismas caracteristicas
- Pares negativos: Dos imágenes que contienen diferentes caracteristicas
def create_pairs(X: np.ndarray, y: np.ndarray):
"""
Args:
X (np.ndarray): Array de imagenes
y (np.ndarray): Array de etiquetas
return:
pairs (np.ndarray): Array de pares de imagenes
labels: Etiquetas de las imagenes, 1 si son pares positivos y 0 si son pares negativos
"""
# image indices by class labels: y
num_classes = max(y) + 1
indices = [np.where(y == i)[0] for i in range(num_classes)]
pairs, labels = [], []
# max number of pairs using the min number of images by class
n = min([len(i) for i in indices]) - 1
for c in range(num_classes):
for i in range(n):
# positive pair
img1 = X[indices[c][i]]
# next image of the same class
img2 = X[indices[c][i+1]]
pairs.append((img1, img2))
labels.append(1.)
# negative pair
# select a random class
neg = np.random.choice([_c for _c in range(num_classes) if _c != c])
# select a random image
img1 = X[indices[c][i]]
img2 = X[indices[neg][i]]
pairs.append((img1, img2))
labels.append(0.)
return np.array(pairs), np.array(labels)
X_train_pair, y_train_bin = create_pairs(X_train, y_train)
X_test_pair, y_test_bin = create_pairs(X_test, y_test)
print(f'train pair: {X_train_pair.shape} and type {X_train_pair.dtype} label: {y_train_bin.shape} type {y_train_bin.dtype}')
print(f'test pair: {X_test_pair.shape} and type {X_test_pair.dtype} labe: {y_test_bin.shape} type {y_test_bin.dtype}')
train pair: (119980, 2, 28, 28) and type float32 label: (119980,) type float64
test pair: (19980, 2, 28, 28) and type float32 labe: (19980,) type float64
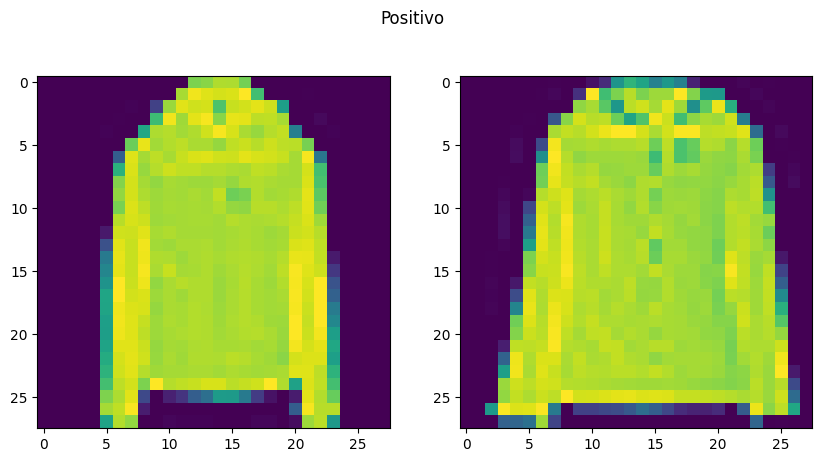
Ya preparamos los pares de datos para entrenar la red neuronal ahora por cada ejemplo en nuestra input tenemos dos images y nuestro output es un valor 0 o 1 dependiendo si son negativos o positivos respectivamente.
Para poder tener un contexto visual graficaremos las imagenes de ejemplo, una a lado de la otra. En el código usamos un random para seleccionar el par de imagenes a mostrar esto se hace para que se pueda jugar por los datos y ver distintos ejemplos.
def plot_pair(pair: np.ndarray, label: float, pred: float = None):
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].imshow(pair[0])
ax[1].imshow(pair[1])
if label:
title = "Positivo"
else:
title = "Negativo"
if pred is not None:
if pred < 0.5:
title += f" - pred: {pred:.2f} - Positivo"
else:
title += f" - pred: {pred:.2f} - Negativo"
fig.suptitle(title)
plt.show()
num_exam = random.randrange(len(X_train_pair))
plot_pair(X_train_pair[num_exam], y_train_bin[num_exam])
Modelo base
input_shape = (28, 28, )
def build_model_base():
input = tf.keras.Input(shape=input_shape, name="base_input")
x = tf.keras.layers.Flatten(name="flatten_input")(input)
x = tf.keras.layers.Dense(128, activation='relu', name="first_base_dense")(x)
x = tf.keras.layers.Dropout(0.1, name="first_dropout")(x)
x = tf.keras.layers.Dense(128, activation='relu', name="second_base_dense")(x)
x = tf.keras.layers.Dropout(0.1, name="second_dropout")(x)
x = tf.keras.layers.Dense(128, activation='relu', name="third_base_dense")(x)
return tf.keras.Model(inputs=input, outputs=x, name="base_model")
model_base = build_model_base()
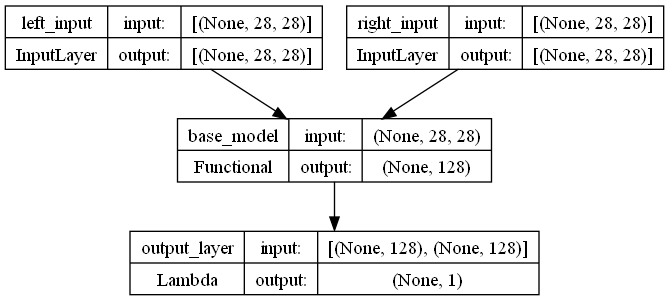
tf.keras.utils.plot_model(model_base, show_shapes=True)

Vamos ahora a construir la Siamense Network, donde podremos ver que tenemos dos entradas que se enviaran a al modelo base y esta pasara por una capa personalizada que calculara la distancia entre los dos vectores de salida de la red base, distancia euclidiana
Distancia Euclidiana
la distancia euclidiana es una medida de distancia entre dos puntos que se puede generalizar a cualquier dimensión. En otras palabras, es la distancia entre dos puntos que se puede medir con una regla. En dos dimensiones, la distancia euclidiana entre los puntos
def euclidean_distance(vects):
import keras.backend as K
vect_a, vect_b = vects
sum_square = K.sum(K.square(vect_a - vect_b), axis=1, keepdims=True)
return K.sqrt(K.maximum(sum_square, K.epsilon()))
def ouput_shape(shapes):
shape1, shape2 = shapes
return (shape1[0], 1)
# create input a
input_a = tf.keras.Input(shape=input_shape, name='left_input')
vect_output_a = model_base(input_a)
# create input b
input_b = tf.keras.Input(shape=input_shape, name='right_input')
vect_output_b = model_base(input_b)
# measure the similarity of the two vectorized outputs
output = tf.keras.layers.Lambda(euclidean_distance, name='output_layer', output_shape=ouput_shape)([vect_output_a, vect_output_b])
# create the model
model = tf.keras.Model([input_a, input_b], output)
tf.keras.utils.plot_model(model, show_shapes=True)
Configurar modelo
def contrastive_loss_with_margin(margin):
def contrastive_loss(y_true, y_pred):
'''Contrastive loss from Hadsell-et-al.'06
http://yann.lecun.com/exdb/publis/pdf/hadsell-chopra-lecun-06.pdf
'''
import tensorflow.keras.backend as K
square_pred = K.square(y_pred)
margin_square = K.square(K.maximum(margin - y_pred, 0))
return (y_true * square_pred + (1 - y_true) * margin_square)
return contrastive_loss
rms = tf.keras.optimizers.RMSprop(learning_rate=0.0001)
model.compile(optimizer=rms, loss=contrastive_loss_with_margin(1), metrics=['accuracy'])
Entrenamos el modelo
history = model.fit([X_train_pair[:, 0], X_train_pair[:, 1]], y_train_bin, epochs=30, batch_size=180, validation_data=([X_test_pair[:, 0], X_test_pair[:, 1]], y_test_bin))
Epoch 1/30
667/667 [==============================] - 6s 7ms/step - loss: 0.1847 - accuracy: 0.2415 - val_loss: 0.1192 - val_accuracy: 0.1572
Epoch 2/30
667/667 [==============================] - 4s 6ms/step - loss: 0.1169 - accuracy: 0.1469 - val_loss: 0.1023 - val_accuracy: 0.1336
Epoch 3/30
667/667 [==============================] - 5s 7ms/step - loss: 0.1039 - accuracy: 0.1306 - val_loss: 0.0955 - val_accuracy: 0.1266
Epoch 4/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0968 - accuracy: 0.1215 - val_loss: 0.0910 - val_accuracy: 0.1217
Epoch 5/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0920 - accuracy: 0.1152 - val_loss: 0.0883 - val_accuracy: 0.1200
Epoch 6/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0880 - accuracy: 0.1096 - val_loss: 0.0851 - val_accuracy: 0.1137
Epoch 7/30
667/667 [==============================] - 4s 5ms/step - loss: 0.0846 - accuracy: 0.1046 - val_loss: 0.0825 - val_accuracy: 0.1064
Epoch 8/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0818 - accuracy: 0.1006 - val_loss: 0.0804 - val_accuracy: 0.1040
Epoch 9/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0794 - accuracy: 0.0970 - val_loss: 0.0786 - val_accuracy: 0.1025
Epoch 10/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0771 - accuracy: 0.0931 - val_loss: 0.0777 - val_accuracy: 0.0988
Epoch 11/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0750 - accuracy: 0.0906 - val_loss: 0.0757 - val_accuracy: 0.0969
Epoch 12/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0733 - accuracy: 0.0877 - val_loss: 0.0746 - val_accuracy: 0.0946
Epoch 13/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0716 - accuracy: 0.0852 - val_loss: 0.0739 - val_accuracy: 0.0930
Epoch 14/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0699 - accuracy: 0.0832 - val_loss: 0.0721 - val_accuracy: 0.0910
Epoch 15/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0684 - accuracy: 0.0813 - val_loss: 0.0720 - val_accuracy: 0.0911
Epoch 16/30
667/667 [==============================] - 4s 5ms/step - loss: 0.0671 - accuracy: 0.0798 - val_loss: 0.0705 - val_accuracy: 0.0858
Epoch 17/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0661 - accuracy: 0.0779 - val_loss: 0.0704 - val_accuracy: 0.0880
Epoch 18/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0648 - accuracy: 0.0764 - val_loss: 0.0699 - val_accuracy: 0.0890
Epoch 19/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0637 - accuracy: 0.0752 - val_loss: 0.0693 - val_accuracy: 0.0877
Epoch 20/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0626 - accuracy: 0.0729 - val_loss: 0.0683 - val_accuracy: 0.0863
Epoch 21/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0616 - accuracy: 0.0724 - val_loss: 0.0683 - val_accuracy: 0.0880
Epoch 22/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0608 - accuracy: 0.0718 - val_loss: 0.0671 - val_accuracy: 0.0845
Epoch 23/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0599 - accuracy: 0.0700 - val_loss: 0.0671 - val_accuracy: 0.0852
Epoch 24/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0591 - accuracy: 0.0698 - val_loss: 0.0670 - val_accuracy: 0.0849
Epoch 25/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0585 - accuracy: 0.0693 - val_loss: 0.0663 - val_accuracy: 0.0843
Epoch 26/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0578 - accuracy: 0.0683 - val_loss: 0.0660 - val_accuracy: 0.0848
Epoch 27/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0568 - accuracy: 0.0671 - val_loss: 0.0659 - val_accuracy: 0.0848
Epoch 28/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0563 - accuracy: 0.0671 - val_loss: 0.0658 - val_accuracy: 0.0852
Epoch 29/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0559 - accuracy: 0.0663 - val_loss: 0.0650 - val_accuracy: 0.0834
Epoch 30/30
667/667 [==============================] - 4s 6ms/step - loss: 0.0553 - accuracy: 0.0663 - val_loss: 0.0655 - val_accuracy: 0.0842
Evaluamos el modelo
pred = model.predict([X_test_pair[:, 0], X_test_pair[:, 1]])
625/625 [==============================] - 1s 2ms/step
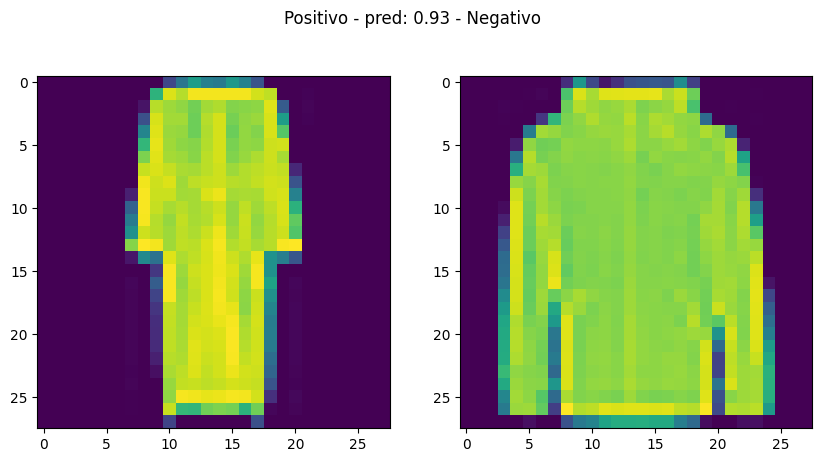
examples = np.random.choice(range(len(pred)), size=5, replace=False)
for i in examples:
plot_pair(X_test_pair[i], y_test_bin[i], pred[i][0])
graficar funcion de perdida
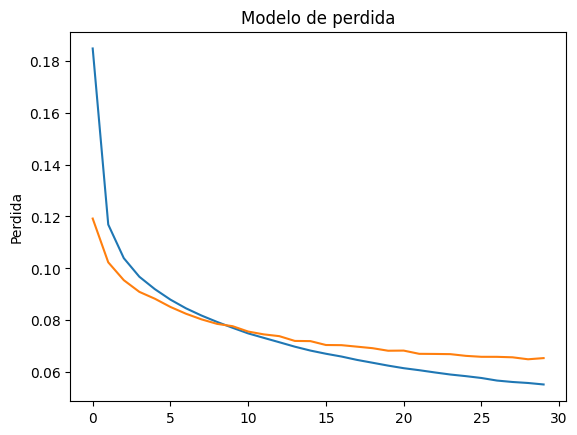
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('Modelo de perdida')
plt.ylabel('Perdida')
plt.show()