Modelo con mutiples salidas
En este notebook, crearemos un modelo con multiples salidas usando el API funcional de keras.
Para el modelo usaremos lo datos de Energy efficiency
Importar modulos
::: {.cell _cell_guid=‘bc1c482a-3443-4deb-bfbe-35775986216c’ _uuid=‘3869d47c-4312-4dae-8587-4c76fe28cb21’ execution=‘{“iopub.execute_input”:“2023-08-11T20:34:57.287840Z”,“iopub.status.busy”:“2023-08-11T20:34:57.286929Z”,“iopub.status.idle”:“2023-08-11T20:34:57.295622Z”,“shell.execute_reply”:“2023-08-11T20:34:57.293802Z”,“shell.execute_reply.started”:“2023-08-11T20:34:57.287795Z”}’ jupyter=‘{“outputs_hidden”:false}’ trusted=‘true’ execution_count=1}
import tensorflow as tf
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
import requests
from io import BytesIO
import zipfile
:::
Preparar los datos
Descargamos el dataset y preparamos nuestros datos de entrenamiento y pruebas
# download file
url = 'https://archive.ics.uci.edu/static/public/242/energy+efficiency.zip'
r = requests.get(url)
zip_data = BytesIO(r.content)
# unzip
with zipfile.ZipFile(zip_data, 'r') as zip_file:
with zip_file.open('ENB2012_data.xlsx') as excel_file:
df = pd.read_excel(excel_file)
# random sort
df = df.sample(frac=1)
df.head()
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | Y1 | Y2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 470 | 0.66 | 759.5 | 318.5 | 220.5 | 3.5 | 4 | 0.25 | 4 | 12.86 | 16.17 |
| 379 | 0.64 | 784.0 | 343.0 | 220.5 | 3.5 | 5 | 0.25 | 2 | 17.11 | 20.43 |
| 31 | 0.71 | 710.5 | 269.5 | 220.5 | 3.5 | 5 | 0.00 | 0 | 6.40 | 11.67 |
| 747 | 0.74 | 686.0 | 245.0 | 220.5 | 3.5 | 5 | 0.40 | 5 | 14.39 | 16.70 |
| 737 | 0.79 | 637.0 | 343.0 | 147.0 | 7.0 | 3 | 0.40 | 5 | 41.96 | 37.70 |
::: {.cell _cell_guid=‘966384d2-52f6-43fe-a9a7-30a34005525c’ _uuid=‘246e7b03-c479-425e-b12e-0d31b6caa74c’ execution=‘{“iopub.execute_input”:“2023-08-11T20:35:01.995196Z”,“iopub.status.busy”:“2023-08-11T20:35:01.994656Z”,“iopub.status.idle”:“2023-08-11T20:35:02.010268Z”,“shell.execute_reply”:“2023-08-11T20:35:02.008886Z”,“shell.execute_reply.started”:“2023-08-11T20:35:01.995155Z”}’ jupyter=‘{“outputs_hidden”:false}’ trusted=‘true’ execution_count=3}
# split data
train, test = train_test_split(df, test_size=0.2)
def format_data(df: pd.DataFrame):
y1 = df['Y1'].values
y2 = df['Y2'].values
X = df.drop(['Y1', 'Y2'], axis=1)
return X, (y1, y2)
X_train, Y_train = format_data(train)
X_test, Y_test = format_data(test)
:::
::: {.cell _cell_guid=‘f867a2c3-849d-476b-8068-deea62ff3ea8’ _uuid=‘3717aebb-1951-47bc-aeb9-ef1ee7af3ced’ execution=‘{“iopub.execute_input”:“2023-08-11T20:35:06.917556Z”,“iopub.status.busy”:“2023-08-11T20:35:06.917099Z”,“iopub.status.idle”:“2023-08-11T20:35:06.925773Z”,“shell.execute_reply”:“2023-08-11T20:35:06.924386Z”,“shell.execute_reply.started”:“2023-08-11T20:35:06.917524Z”}’ jupyter=‘{“outputs_hidden”:false}’ trusted=‘true’ execution_count=4}
# normalize data
scaler = preprocessing.StandardScaler()
X_train_norm = scaler.fit_transform(X_train)
X_test_norm = scaler.transform(X_test)
:::
El modelo
Ahora construiremos nuestro modelo teniendo en cuenta que va a tener dos salidas
def build_model():
input_layer = tf.keras.layers.Input(shape=(8,))
hidden_layer = tf.keras.layers.Dense(128, activation='relu')(input_layer)
hidden_layer = tf.keras.layers.Dense(128, activation='relu')(hidden_layer)
# ouput 1
y1 = tf.keras.layers.Dense(1, name='y1')(hidden_layer)
# output 2
hidden_layer = tf.keras.layers.Dense(64, activation='relu')(hidden_layer)
y2 = tf.keras.layers.Dense(1, name='y2')(hidden_layer)
return tf.keras.models.Model(inputs=input_layer, outputs=[y1, y2])
Graficar nuestro modelo
Vamos a graficar nuestro modelo donde podemos observar de forma mas
simple nuestras dos salidas y1 y y2, tambien podemos ver que y2
tiene una capa extra, esta es la de
tf.keras.layers.Dense(units=1, name='y2', activation='linear')(X)
model = build_model()
model.summary()
Model: "model"
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_1 (InputLayer) [(None, 8)] 0 []
dense (Dense) (None, 128) 1152 ['input_1[0][0]']
dense_1 (Dense) (None, 128) 16512 ['dense[0][0]']
dense_2 (Dense) (None, 64) 8256 ['dense_1[0][0]']
y1 (Dense) (None, 1) 129 ['dense_1[0][0]']
y2 (Dense) (None, 1) 65 ['dense_2[0][0]']
==================================================================================================
Total params: 26,114
Trainable params: 26,114
Non-trainable params: 0
__________________________________________________________________________________________________
Configurar parametros
model.compile(
optimizer=tf.optimizers.SGD(learning_rate=0.001),
loss={
'y1': tf.keras.losses.MeanSquaredError(),
'y2': tf.keras.losses.MeanSquaredError(),
},
metrics={
'y1': tf.keras.metrics.RootMeanSquaredError(),
'y2': tf.keras.metrics.RootMeanSquaredError(),
}
)
Entrenar el modelo
model.fit(
X_train_norm, Y_train,
epochs=500, batch_size=10,
validation_data=(X_test_norm, Y_test),
verbose=0
)
<keras.callbacks.History at 0x1e161d1ed10>
Evaluar el modelo
Ahora vamos a evaluar el modelo y graficar los datos para tener una mejor idea de lo que esta pasando
model.evaluate(X_test_norm, Y_test)
5/5 [==============================] - 0s 2ms/step - loss: 0.9150 - y1_loss: 0.2067 - y2_loss: 0.7082 - y1_root_mean_squared_error: 0.4547 - y2_root_mean_squared_error: 0.8416
[0.9149883389472961,
0.2067471146583557,
0.7082412838935852,
0.454694539308548,
0.8415707349777222]
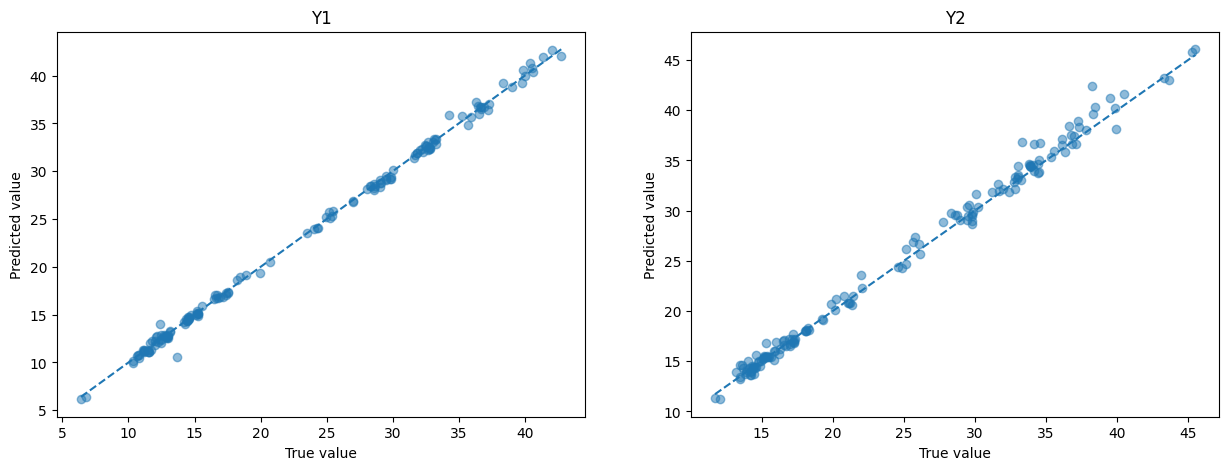
Comparar datos reales y predichos
pred = model.predict(X_test_norm)
print(pred[0][:5])
Y_test[0][:5]
5/5 [==============================] - 0s 1ms/step
[[33.359097]
[37.002422]
[23.915794]
[35.689697]
[24.020735]]
array([33.16, 37.26, 24.03, 35.94, 24.24])
def plot_values(ax, y_true, y_pred, title):
ax.scatter(y_true, y_pred, alpha=0.5)
ax.plot([y_true.min(), y_true.max()], [y_true.min(), y_true.max()], '--')
ax.set_xlabel('True value')
ax.set_ylabel('Predicted value')
ax.set_title(title)
# Y1 vs pred
fig, ax = plt.subplots(1, 2, figsize=(15, 5))
plot_values(ax[0], Y_test[0], pred[0], 'Y1')
plot_values(ax[1], Y_test[1], pred[1], 'Y2')