Arbol de Desición, conceptos básicos

Modelo de arbol de desición

Un árbol de decisión es un modelo de predicción utilizado en el ámbito de la inteligencia artificial, que utiliza un árbol de estructura similar a los diagramas de flujo en donde cada nodo representa una característica (o atributo), cada rama representa una regla de decisión y cada hoja representa el resultado de una decisión. Los árboles de decisión son utilizados comúnmente en minería de datos con el fin de resolver problemas de clasificación.

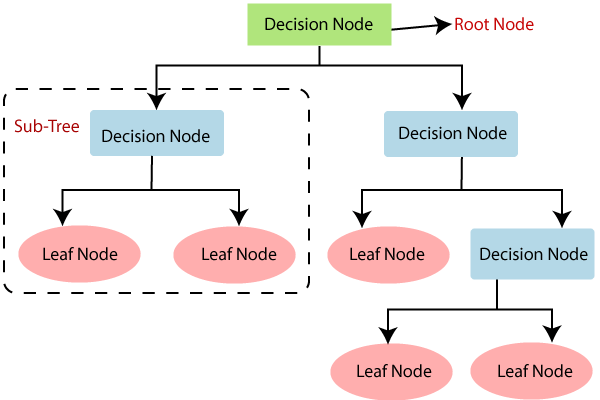
Ejemplo de un arbol de desición y su estructura:

Entropía

¿Qué es la entropía?

La entropía es una medida de incertidumbre. En el contexto de la toma de decisiones, la entropía mide la impureza de un conjunto de ejemplos S. Si S solo contiene ejemplos de una clase, entonces la entropía es 0. Si S contiene una cantidad uniforme de ejemplos de cada clase, entonces la entropía es 1. La entropía de un conjunto S se denota por H (S).

¿Cómo se calcula la entropía?

La entropía de un conjunto S se calcula como:

$H(S) = -\sum_{i=1}^{c} p_i log_2 p_i$

Donde:

• $c$ es el número de clases
• $p_i$ es la proporción de ejemplos de clase $i$ en $S$
• $log_2$ es el logaritmo en base 2

Ejemplo de cálculo de entropía

Supongamos que tenemos un conjunto de ejemplos $S$ con 14 ejemplos de clase 1 y 6 ejemplos de clase 2. La entropía de $S$ es:

$P_1 = 14/20$ y $P_2 = 6/20$

Entonces, la entropía de $S$ sería: $H(S) = - \left(\frac{14}{20} \log_2 \frac{14}{20} + \frac{6}{20} \log_2 \frac{6}{20}\right) \approx 0.88$.

Ganancia de información

La ganancia de información(IG) se utiliza para decidir qué atributo se utilizará para dividir el conjunto de datos en subconjuntos homogéneos. La ganancia de información se define como la diferencia entre la entropía antes de la división y la entropía después de la división por un atributo. La ganancia de información se denota por IG (S, A) y se calcula como:

$IG(S, A) = H(S) - \sum_{v \in Values(A)} \frac{|S_v|}{|S|} H(S_v)$

Donde:

• $S$ es el conjunto de ejemplos
• $A$ es el atributo utilizado para dividir $S$ en subconjuntos
• $Values(A)$ es el conjunto de valores que puede tomar el atributo $A$
• $S_v$ es el subconjunto de $S$ en el que el atributo $A$ tiene el valor $v$

Indice Gini

El índice de Gini es una medida de impureza utilizada en los árboles de decisión para decidir qué atributo dividir un nodo en dos o más subnodos. El índice de Gini se define como:

$Gini(S) = 1 - \sum_{i=1}^{c} p_i^2$

Donde:

• $c$ es el número de clases
• $p_i$ es la proporción de ejemplos de clase $i$ en $S$

Pros y contras de los árboles de decisión

Pros

• Fácil de entender e interpretar. Los árboles se pueden visualizar.
• Puede ser muy util para solucionar problemas relacionados con decisiones.
• Hay menos requisitos de limpieza de datos

Contras

• Los árboles de decisión pueden ser poco precisos. Pueden ser muy sensibles a pequeños cambios en los datos.